本文基本上就是 Optimal Preprocessing for Answering On-line Product Queries 和 Data Structures for Range Minimum Queries in Multidimensional Arrays 的非形式化翻译，掺杂了自己的理解和思路，略去了一些细节。

主要讲一下比较基础的静态数组、高维数组的区间查询问题。两篇论文其实关系不大，只是后一篇用了前一篇的部分成果。

理论性比较强，尤其是后一篇，基本上出不成题。

静态序列区间半群查询问题

问题：给定半群元素序列 $a_{1\cdots n}$，在只能使用半群运算 $\circ$ 的情况下，多次询问区间 $[l,r]$，回答 $\circ_{i=l}^r a_i$。

解决思路无非就是预处理一些区间的积，查询时拼起来就行。联想到正常的动态区间查询问题，动态情况下下界就是 $\Omega(\log n)$ 的。静态情况下允许的预处理量大大增加，因此分析下去会不一样，但思路还是可以借鉴的。总体来说，核心的思想就是两点：

1. 预处理与查询的平衡。
2. 分块与分治。

记 $k$ 表示回答查询时允许的半群运算次数 ${}+1$。

最初的思考从 $k=2$ 开始（$k=1$ 只能预处理所有平方个区间），我们要给每个区间 $[l,r]$ 选定一个切分点，然后进行所需的预处理。为了使公共预处理区间尽量多，考虑每次选择一个点，将所有尚未确定切分点，且能以该点为切分点的区间的切分点选定为该点。这个就是猫树，下面说点题外话。

记猫树的预处理量为 $p(n)$。每次选取中点作为切分点的最优性是由 $p(n)$ 的凸性保证的。我们可以通过解递归式得到：

$$ p(n)=n\lfloor\log_2(n-1)\rfloor+2n-2^{\lfloor\log_2(n-1)\rfloor+1} $$

为了方便 $\mathrm{O}(1)$ LCA，猫树有少量冗余。理论上递归可以只进行 build(l,mid-1) 和 build(mid+2,r)，并且在 $r-l\le 1$ 时结束，记猫树最优的预处理量为 $p'(n)$：

$$ p'(n)=(n+2)\lfloor\log_2(n+1)\rfloor-n+2-2^{\lfloor\log_2(n+1)\rfloor+1} $$

猜想：对于长为 $n$ 的序列，$k=2$ 情况下符合条件的预处理区间集合 $\mathcal{P}$，除去 $n$ 个单元素区间，${\lvert\mathcal{P}\rvert}_\min=p'(n)$。

注意这里的最优性和上文的最优性是不一样的，上文是“每次选择一个切分点，然后两边递归”这个思路前提的基础上的最优性。

纠结于系数意义不大，我们关注 $k=2$ 情况的结构带来的启发。“预处理前/后缀和”是非常有效的线性手段。

但是如何推理 $k>2$ 呢？众所周知，动态情况下的线段树是从分块嵌套演化过来的，因此考虑类比逆推多个切分点的情况（只预处理每一块内的前后缀和）：

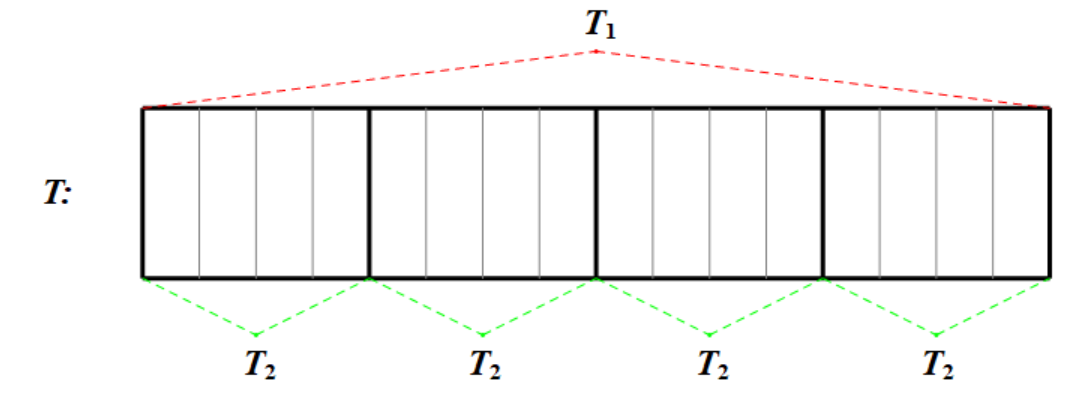
对于一个询问，如果它在块内部，则递归 $T_2$ 处理，否则两头散块可以用前后缀和算出，然后考虑 $T_1$ 用于维护每块的和形成的较短序列，处理块间部分。

记块大小为 $B(n)$，预处理复杂度为 $p(n)$，回答询问使用的运算次数最多为 $q(n)-1$。下文中可能出现多个 $f(n)$，作用域仅在单自然段内。

利用分治的思想，考虑三种可能（记 $q(n)=k$ 的数据结构为 $S_k$，$S_2=$ 猫树）：

1. $T_1=T,T_2=T$。
   $p(n)=p(n/B(n))+n/B(n)\cdot p(B(n))+\Theta(n),q(n)=\max\{q(n/B(n))+2,q(B(n))\}$，上下均自递归的结构其实很像 vEB 树，因此考虑取 $B(n)=\sqrt n$，将 $p(n)$ 展开后使用初中处理因式的技巧，就可以得到 $p(n)=\Theta(n\log\log n)$，同时 $q(n)=\Theta(\log\log n)$。我猜测无法更优了。
2. $T_1=T,T_2=S_2$。
   $p(n)=p(n/B(n))+\Theta(n\log B(n)),q(n)=q(n/B(n))+2$，可以对输入的固定的 $n$ 取 $\forall i,B(i)=2^\sqrt{\log n}$，这样可以平衡成 $p(n)=\Theta\left(n\sqrt{\log n}\right),q(n)=\Theta\left(\sqrt{\log n}\right)$。这个方向没有前途的直觉解释是：分块后问题分成了 $T_1$——单个规模较小、$T_2$——若干规模很小，但总和不变 这两个子问题，直觉上后者是比前者难的，拿已有的结构作为 $T_2$ 基本没法优化。
3. $T_1=S_2,T_2=T$。
   $p(n)=\Theta(n/B(n)\cdot\log(n/B(n)))+n/B\cdot p(B(n))+\Theta(n),q(n)=4$，很明显可取 $B(n)=\log n$，从而做到 $p(n)=\mathrm{O}(n\log^*n)$，这个就是 $S_4$。

第三种可能实际上提供了一个以 $q(n)$ 增加 $2$ 为代价，将 $p(n)=\mathrm{O}(n\cdot f(n))$ 变为 $\mathrm{O}(n\cdot f^*(n))$ 的通法（得满足 $f(n)=\mathrm{O}(\log n)$，取 $B(n)=f(n)$ 即可），其中 $f^*(n)=\min\{i\mid f^{(i)}(n)\le 1\}$。 因此我们可以做到： $$ \forall 2\mid k\ge 4,p(n)=\mathrm{O}(n\log^{\begin{matrix}k/2-1\\\overbrace{**\cdots *}\end{matrix}}n),q(n)=k $$ ……吗？

这里有一个很容易犯的错误，就是如果不用主定理解递归式，那么解的过程中严谨地来说必须避免渐进记号。但 OI 实践中往往不拆也不会出问题，这里实际上套上了一个归纳，并且把 $k$ 作为变量塞进渐进记号里了，就得谨慎地算一下了。$k=4$ 时：

$$ \begin{aligned} p(n)&=n/\log n\cdot \log(n/\log n)+n/\log n\cdot p(\log n)+2n-2\log n\\ &<3n+n/\log n\cdot p(\log n)\\ &=3n\log^* n \end{aligned} $$

同理，可以算得 $k=6$ 时 $p(n)<5n\log^*n$ 等等。因此：

$$ \forall 2\mid k\ge 4,p(n)=\mathrm{O}(n\textcolor{red}{k}\log^{\begin{matrix}k/2-1\\\overbrace{**\cdots *}\end{matrix}}n),q(n)=k $$

另外，为了完整，我们把 $2\nmid k$ 也补上。$k=3$ 套上 $T_1=S_1$，（特例）取 $B(n)=\sqrt n$，可以得到 $p(n)=\Theta(n\log\log n)$ 的 $S_3$，$k\ge 5$ 就跟 $k-1$ 情况一样了。

为了平衡 $p(n)/n$ 和 $q(n)$，考虑取 $k=2\alpha(n)+2$，其中：

$$ \alpha(n)=\min\{i\mid\log^{\begin{matrix}i\\\overbrace{**\cdots *}\end{matrix}}n\le 3\} $$

这里 $\le 3$ 时因为 $n\ge 5$ 时不管有几个星，结果都至少是 $3$。您可能在其他地方见过 $\alpha(n)$ 的不同定义方式，不同的定义应该都只差一个常数。

这时 $p(n)=\mathrm{O}(n\alpha(n)),q(n)=\Theta(\alpha(n))$。注意这里的 $\alpha(n)$ 是无法变成 $\alpha^*(n)$ 的，但是有另一个看起来不大优美的优化方式：

仍然考虑上文的分块模型，$T_1=S_{2\alpha(n)+2},T_2=T_{?}$，设 $T_{?}$ 的预处理时间为 $p_{?}(n)=\mathrm{O}(n\cdot f(n))$。那么总的 $p(n)=\mathrm{O}(n/B(n)\cdot\alpha(n)+n\cdot f(B(n)))$，如果要使得 $p(n)=\Theta(n)$，唯一的方法是取 $B(n)=\alpha(n),f(n)=\mathrm{O}(1)$，那么 $T_{?}$ 可以选择普通线段树。好在这部分的询问运算次数不是瓶颈，因此总的 $q(n)$ 只会加 $2$（最外层两端的散块）。这里主要是通过类似于待定系数法的方式解释一下论文里为什么会突然冒出普通线段树。

这个优化的思想是，用“单个规模较小”优化预处理“常数”（红色的 $k$），“若干规模很小，但总和不变”尽管无法有效减小预处理复杂度，但是可以保证查询次数足够少。二者互补。

我尝试类推优化掉任意 $k$ 的“常数”（红色的 $k$）（这个原论文里没讲），但 $q(n)$ 会加 $2$。这个是可以避免的：

希望 $q(n)=k\ge 3$，最外层是 $T_1=S'_k,T_2=普通线段树,B(n)=k$。$S'_k$ 是修改过的结构，基本与 $S_k$ 相同，即 $T_1=S_{k-2},T_2=S'_k,B(n)=f(n)$，这里 $f(n)$ 指的是设 $S_{k-2}$ 的预处理复杂度为 $\mathrm{O}(n(k-2)f(n))$。不同的点在于 $S'_k$ 处理的块内前后缀和是细分到原序列的，而不是严格遵循最外层分块结构把每 $k$ 个一组的和视为整体。这样就避免了最外层跨块时额外查一对前后缀和。$S'_k$ 的预处理复杂度仍然是 $p(n)=\mathrm{O}(nk/B(n)\cdot f(n))+n/B(n)\cdot p(B(n))+\Theta(nk)=\mathrm{O}(nk\cdot f^*(n))$，其他部分也都没有问题，总体来说就把 $p(n)$ 的 $k$ 除掉了，$q(n)$ 不变。最终我们得到了：

$$ p(n)=\begin{cases}\mathrm{O}(n^2)&q(n)=1\\\mathrm{O}(n\log n)&q(n)=2\\\mathrm{O}(n\log\log n)&q(n)=3\\\mathrm{O}(n\log^{\begin{matrix}\lfloor k/2\rfloor-1\\\overbrace{**\cdots *}\end{matrix}}n)&q(n)=k\ge 4\end{cases} $$

但如果具体实现真想做到查询时间复杂度 $=\Theta(q(n))$，那就得处理一个“变进制数 LCP 问题”，而且 $q(n)\ge 4$ 后基本没法体现区别，所以只能套一个交互限制运算次数或者像 【北大集训2021】末日魔法少女计划 这样。

下界的证明思路是对着这个分块结构硬证。对于 $k=2$，选择序列中点 $m$，将只包含于中点左侧（不含中点）和只包含于中点右侧（不含中点）的预处理作为一类，跨左右的预处理作为一类。考虑询问 $[m-i,m+i]$，要用两个预处理拼成该询问，就必须有一个跨左右的预处理。因此 $p(n)\ge p(\lfloor n/2\rfloor)+p(\lceil n/2\rceil-1)+\lceil n/2\rceil-1$，解得 $p(n)=\Omega(n\log n)$。对于 $k\ge 3$，按 $S_k$ 的块大小分块，但块间空出一位。也是先忽略块内的预处理，剩余跨块的预处理。对于一个位置，如果它不是任何跨块预处理的端点，则标记它。如果含有被标记位置的块不足一半，那么跨块预处理至少 $\Omega(n)$；超过一半，那么考虑所有以标记位置为两端的询问，组成询问区间的最左右预处理一定是块内的，去掉这两部分后剩余问题一定不弱于 $k'=k-2,n'=n/B(n)$ 情况的问题，跨块预处理也是至少 $\Omega(n)$，归纳即可，这里注意不会带有因子 $k$。论文里提到这个证明可以直接推广成“预处理可以是任意子集且不要求不交并”情况。

因此，上述解法的半群运算次数是渐进最优的。论文标题上加了个 on-line，不知离线是否会有更好的结果。

高维 RMQ 问题

问题：给定高维数组 $a_{1\cdots n_1,\cdots,1\cdots n_d}$，在只能使用比较运算的情况下，多次询问高维区间 $[l_1,r_1],\cdots,[l_d,r_d]$，回答 $\min_{i_1\in[l_1,r_1]}\cdots\min_{i_d\in[l_d,r_d]}\{a_{i_1,\cdots,i_d}\}$。记 $N=\prod n_i$。

以下视 $d$ 为定值，但还是会尽量写一下关于 $d$ 的常数。以下假设 $a$ 中数互不同。

先尝试把上文的静态区间半群查询问题的 $S_k$ 扩展到 $d$ 维结构 $S_k^d$：非常简单，处理块内前后缀和时，不再是存储单个元素，而是一个 $d-1$ 维数组，就需要嵌套下去，那就归约 $S_k^{d-1}$ 了。时间复杂度的变化是预处理的 $\log$ 以及查询会带上 $d$ 次方。

目前可以做到的是预处理 $\mathrm{O}(N\log^{d-1}N)$，查询 $\mathrm{O}(2^d)$，也就是把最内层一维套个四毛子。

但是我们的目标是预处理 $\Theta(N)$，查询 $\mathrm{O}(1)$。可以推理得到以下几点：

1. 得用四毛子。
2. 直接用 $S_2^d$ 之类的结构肯定不行。

那如果是 $S_3^d$ 的最内层套四毛子，是不是就可以做到 $\mathrm{O}\left(N\frac{(\log\log N)^d}{\log N}\right)=\mathrm{o}(N)$ 了呢？答案是否定的，因为次内层的结构是带一个前后缀 $\min$ 的，也就是要得到最内层建树所基于的序列，就先得乘 $\Theta(n_d)$，而其他外层又无法直接套四毛子，所以如果用这种思路，就必定是 $\Omega(N(\log\log N)^{d-1})$ 的。因此一维的四毛子不行。

四毛子的关键是找到一个信息量足够小的贴近本质的刻画，那如何找到一个高维数组的所有可能的区间 $\min$ 的刻画呢？不幸的是，论文中提到，二维的 $n\times n$ 方阵不存在类笛卡尔树的刻画，因为在矩形 $\min$ 查询意义下本质不同的方阵个数为 $\Omega(((n/4)!)^{n/4})$，取对数发现光是靠比较来区分所有的情况都无法做到 $\mathrm{O}(n^2)$。

一种新的刻画一维序列的方式如下：考虑猫树，树的每个节点预处理所有前后缀 $\min$。尽管建树复杂度无法做到 $\Theta(n)$，但比较次数是可以的：考虑一个节点的前缀 $\min$，前一半从左儿子继承，后一半从右儿子继承的同时，要与左儿子 $\min$ 再取个 $\min$，而这个取 $\min$ 的决策情况显然可以二分分界点，因此一个节点的比较次数可以做到长度的对数，总体来说就是至多 $2\sum_{i\ge1}i\cdot\frac{n}{2^i}=4n$ 次。

猫树可以扩展到高维 $S_2^d$，但为了保证比较次数，处理方法要稍作调整：对于某个节点，设其对应的区间长度为 $2^{i_1}\times\cdots\times 2^{i_d}$，由于不能多维同时二分，故选择最长的一维，将这一维切成两半后对应的节点信息作为继承 $\min$ 值的来源，其他维暴力扫描，这一维二分。比较次数为（这里的 $2^d$ 是每一维都要前后缀）：

$$ \begin{aligned} &\sum_{i_1,\cdots,i_d}\max_j\{i_j\}\cdot\frac{\prod_j2^{i_j}}{\max_j\{2^{i_j}\}}\cdot 2^d\cdot\frac{N}{\prod_j2^{i_j}}\\ =&\,2^dN\sum_{i_1,\cdots,i_d}\frac{\max_j\{i_j\}}{2^{\max_j\{i_j\}}}\\ =&\,2^dN\sum_i\frac{i}{2^i}\left[(i+1)^d-i^d\right]\\ <&\,2^dN\sum_i\frac{i^{d+1}}{2^{i-1}}\\ =&\,2^{d+2}N\cdot \tilde{b}(d+1)\\ \approx&\,\frac{2^{d+1}(d+1)!}{(\ln 2)^{d+2}}N\\ =&\,\Theta(N) \end{aligned} $$

其中 $\tilde{b}(n)$ 是 A000670。注意如果不选最长的一维切就不能线性了。

由于这个结构并非确定唯一的最小值位置，而是给出 $\mathrm{O}(2^d)$ 个候选最小值，故它的线性复杂度并不与上文所说的“无法刻画”矛盾。

好，现在选取边长为 $B=c\log^{1/d}N$ 的 $d$ 维超立方体作为小块，使用四毛子（为了快速识别输入的每一小块的类型，避免带上 $\log^d$，可以选取足够小的常数 $c$，$\mathrm{O}(N)$ 地预处理出判断块类型的决策树）。这种分块方式不是严格意义上的高维嵌套分块，需要重新考虑如何回答询问。

注意到，只要询问有一个维度的区间是跨块，那么整块部分就可以直接利用除以 $\log^{1/d} N$ 这个因子，套上 $S_3^d$ 从而达到 $\Theta\left(\max\left\{N,N\frac{(\log\log N)^d}{\log^{1/d}N}\right\}\right)$ 也就是 $\Theta(N)$（因为 $d$ 是定值）；查询的每一维都是块内的情况不必多说。

现在就剩下跨块时去掉中间整块后，散块即两端块内前后缀部分的处理。

论文中给出的方法是：对跨块的这一维的所有块内前后缀 $\min$（指的是多个内层 $d-1$ 维数组对应位置分别取 $\min$），递归建 $d-1$ 维时的原问题结构。总体来说，需要预处理以下三部分：

1. 每个小块的类型；
2. 每一维求出每个块的 $\min$（$B$ 个内层 $d-1$ 维数组对应位置分别取 $\min$），然后建 $S_3^d$。
3. 每一维求出每个块内前后缀的 $\min$，然后递归建 $d-1$ 维的结构。

询问时，如果所有维度都是块内，则直接回答，否则任选一个跨块维度，拆成三个部分处理。

预处理复杂度 $p(n)=\Theta(2^d\tilde{b}(d+1)N)$，具体算一下会发现递归减一维的部分并不是瓶颈，识别小块类型才是。查询 $q(n)=\mathrm{O}(3^d)$。

我想到的一个更简单的方法是：只预处理上文中 1 和 2 结构，$p(n)$ 不变。查询时利用 RMQ 可以重复考虑同一个数的性质，分别考虑每一个跨块的维度，忽略其散块部分（其他维保留原询问区间），在 2 结构中查询，这个是 $\mathrm{O}(d3^d)$；剩余未考虑的就是每一维都是散块的部分，一共有 $\mathrm{O}(2^d)$ 个（左右段各一个）块，每个小块 $\mathrm{O}(2^d)$，乍一看是 $\mathrm{O}(4^d)$，但实际上如果一个维度跨块了，它会给查询数量贡献 $\times 2$，但在高维猫树中由于这维查的是前后缀，所以对候选最小值数量就不贡献 $\times 2$ 了，因此还是 $\mathrm{O}(2^d)$。最终 $q(n)=\mathrm{O}(d3^d)$。